Securing private keys with a high-performance, threshold signature-based protocol

This post is about the paper “Improving security for users of decentralized exchanges through multiparty computation”, by Robert Annessi and Ethan Fast.

The paper introduces an effective algorithm for secure, collaborative signature generation using threshold signatures, and an API-key based client/server protocol that allows user-specific limits and restrictions as well as key revocations and rotations.

The method supports all blockchains that use ECDSA and EdDSA signatures, which includes Bitcoin, Ethereum and the majority of popular cryptocurrencies.

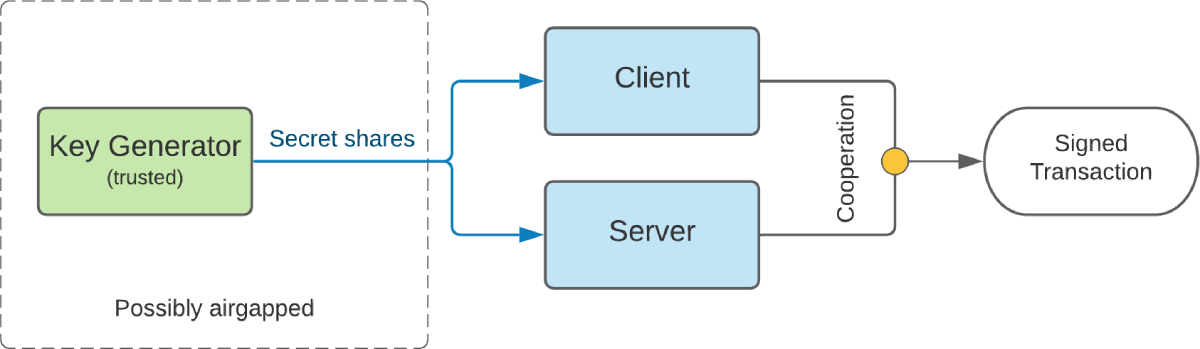
TLDR: Tired of dealing with private keys? Split it into two secret shares and require collaboration of two parties to generate the final signature, with neither party ever knowing the private key.

Cooperation flow for creating a signature

Only the key generator has access to the private key

This setup allows any party to decline cooperation, providing a way to impose user-specific limits, restrictions and requirements for creating signatures, as well as the ability to permanently revoke keys. For one private key, many unique pairs of secret shares can be generated (2256 to be specific).

Secret shares can be created offline / airgapped as in the figure above, or as part of a trusted client or server, depending on your architecture and security profile.

This scheme can be used to secure existing addresses in most blockchains, and can be easily integrated into many applications that currently use private keys.

The costs of this approach (versus just using a private key) include a separate generation step for the secret shares (and possibly transfer onto client and server), required network connectivity between client and server, and stable server operations (because a client can’t create signatures without a working server).

Malicious server software could decline cooperation, but transaction data cannot be modified and reach a valid final signature without agreement (signing) by the other party.

Some areas of application:

  • Applications that create signatures with private keys.
  • Backends and services that interact with blockchains, dapps and wallets.
  • Application-specific client interfaces and GUIs.
  • Hardware wallets like Ledger and Trezor (the private keys could reside on a separate device like a YubiKey).
  • Companies that want a more secure management of their private keys.

User-specific restrictions could include:

  • Transaction details like amounts, recipients, data, …
  • User IP address or location.
  • Trading limits and market restrictions.
  • Withdrawal addresses and limits (even daily / weekly / monthly), time delayed withdrawals.
  • Allow access only from specific devices.
  • Biometric information such as a fingerprint scan.
  • Application-specific logic that can be checked on the server component (whatever can produce true or false as output).

About the paper

The paper presents an in-depth description of the scheme, cryptography and algorithms used, and provides a solid implementation blueprint. It comes with an example implementation in Rust.

Specifically the paper contains the following parts:

  • Review and discussion of existing threshold signature algorithms
  • Improvements of existing 2-of-2 threshold signature algorithms, in particular Lindell’s scheme.
  • Description of an API-key protocol that allows user-specific restrictions and limits, as well as key revocation and rotation.
  • Technical implementation guide for decentralized exchanges.
  • Description of the specific implementation at Nash.

Technical details

The proposed algorithm is an optimized 2-of-2 threshold signature algorithm with significant improvements over Lindell’s scheme. It supports ECDSA and EdDSA signatures.

The process includes two steps (phases):

  • Preparation - The private key is split into two multiplicative secret shares in advance, possibly airgapped, and transferred onto client and server.
  • Finalization - Completing the signature (in a single message between client and server).

Improvements over Lindell’s scheme:

  • Splitting the process into two steps, thereby reducing computational overhead at finalization and allowing airgapped generation of secret shares.
  • Finalization requires only a single message between client and server, and takes about 4ms (and network delay).
  • Lower message size:
    1. Preparation phase: 2x 33 B
    2. Finalization phase: 545 B
  • Lower storage overhead:
    • On the server: 65 B per prepared point (33 B for the compressed point representation and 32 B for the server’s DH secret)
    • On the client: 321 B per prepared point (33 B for the compressed point representation, 32 B for the client’s DH secret, and 256 B for the Paillier randomness)

Summary

The authors present a novel, optimized cryptographic signing scheme which splits a private key into two secret shares and requires collaboration of two parties for creating a signature. The paper also introduces a server/client architecture with minimal communication overhead and API-key based credentials. This setup allows implementation of user-specific limits and restrictions, as well as key revocations and rotations.

When creating the secret shares outside of client and server, at no point does any party have access to the private key or could create signatures without the other party collaborating. If one party is compromised, no signature can be created without the corresponding second secret share.

The paper includes a review of existing threshold signature schemes, specific improvements to Lindell’s scheme, an api-key like signing setup, an implementation blueprint and an example implementation in Rust.

References

Thanks to Robert Annessi and Ethan Fast for reading drafts of this post.

Chris